Measuring \( H_0 \)
with strong lenses
Christoph Becker (Durham/ICC)
Nan Li (Nottingham)


2019.06.11
The Value of \( H_0 \)
- Powerful probe of dark energy
- neutrino physics
- Indications of new physics
(e.g. Sekiguchi+10, Linder11, Freedman+12, Weinberg+12)
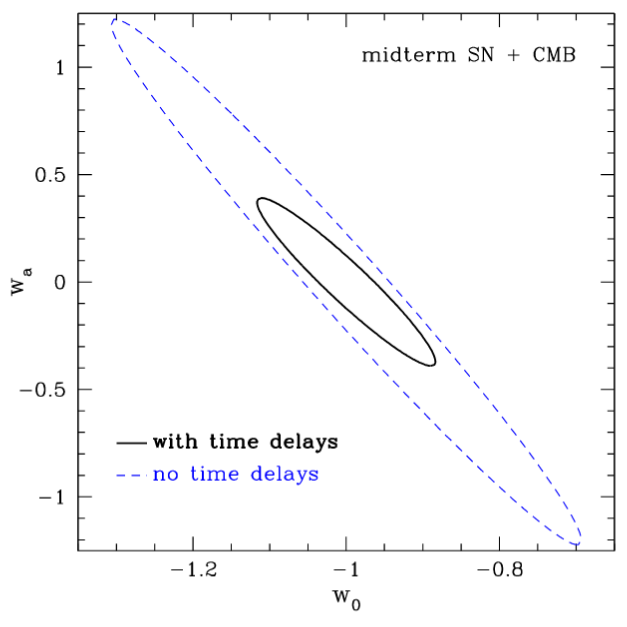
E.V.Linder 11
The Value of \( H_0 \)
- Powerful probe of dark energy
- neutrino physics
- Indications of new physics
(e.g. Sekiguchi+10, Linder11, Freedman+12, Weinberg+12)
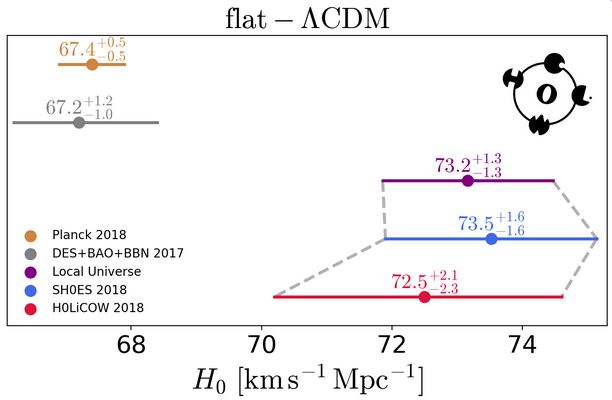
shsuyu.github.io/H0LiCOW/site/, 2019
Independent methods are needed to overcome systematics, especially the unknown unknowns.

Variable sources: e.g. SNe, Quasars
\( H_0 \) from Time-Delays
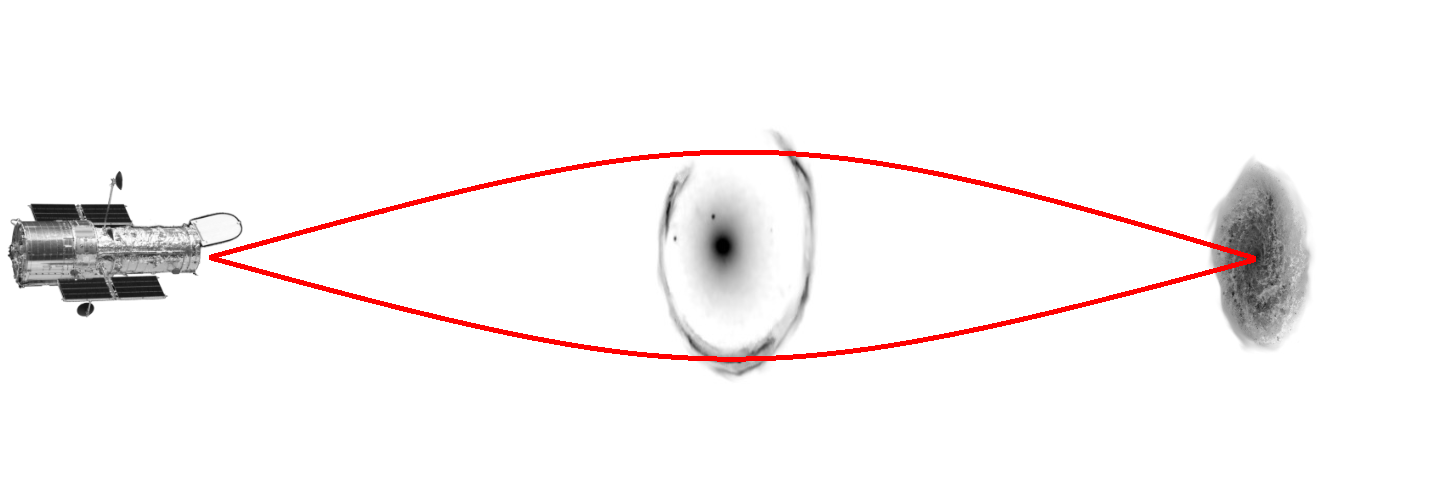
Advanteges:
- simple geometry & well-tested physics
- one-step measurement of cosmological distance
Time Delay
Time Delay Distnace
Lens potential

\( H_0 \) from Time-Delays
\( H_0 \) from Time-Delays

\( D_l \)
\( D_s \)
\( D_{ls} \)
Observable
Goal
Inferable
Effect of LOS-Structures
More l.o.s. structures larger \( {\color{blue}\kappa_{\text{ext}}} \) larger \( {\color{blue}D_{\Delta t}} \)
Observable
Goal
Inferable

Angular diameters are perturbed by large scale structure relative to the homogeneous prediction
Estimating \( \kappa_{\text{ext}} \)
- Compare relative galaxy number counts to cosmological simulations to calibrate \( \kappa_{\text{ext}} \) (e.g., Fassnacht+2011; Greene+2013; Suyu+2010,2013)
- Deep multi-band imaging to get photometric redshift and stellar masses to reconstruct line of sight mass distribution (Rusu+2017)
- Multi-object spectroscopy to characterise nearby galaxies, groups (Sluse+2017)
- Independent \( \kappa_{\text{ext}} \) constraint using weak lensing data (Tihhonova+2018)
Estimating \( \kappa_{\text{ext}} \)
LSST will find 3000 strong lensed quasars with time-delays
(Oguri&Marshall 10)
Estimating \( \kappa_{\text{ext}} \)
LSST will find 3000 strong lensed quasars with time-delays
Impossible to have follow up wide, deep, spectroscopic imaging for all of them!
(Oguri&Marshall 10)
Find \( H_0 \)-\( \kappa_{\text{ext}} \) Relation
1. Construct light-cone with & without LOS-structure
3. Lens mass modelling
2. Ray-tracing through the light-cone
4. \( H_0 \) estimation
Light-Cone
Semi-Analytic model cosmoDC2*:
- designed for LSST-DESC
- based on Outer Rim Simulations (dark-matter only)
- \( \Lambda \)CDM cosmology: \( H_0 = 0.71 \)
- sky coverage = \( 500 \text{deg}^2 \)
- \( z = 0 - 3 \)
- Halo mass = \( 10^{10} - 10^{15} M_{\odot} \)
- Stellar mass = \( 10^{8} - 10^{13} M_{\odot} \)
- including positions, redshift, orientations, ellipticity, colors of the galaxies in a given light cone
*github.com/LSSTDESC/cosmodc2
Light-Cone


\( z_{\text{obs}} \)= 0.0 \( z_{\text{lens}} \)= 0.5 \( z_{\text{src}} \)= 2.0
Light-Cone
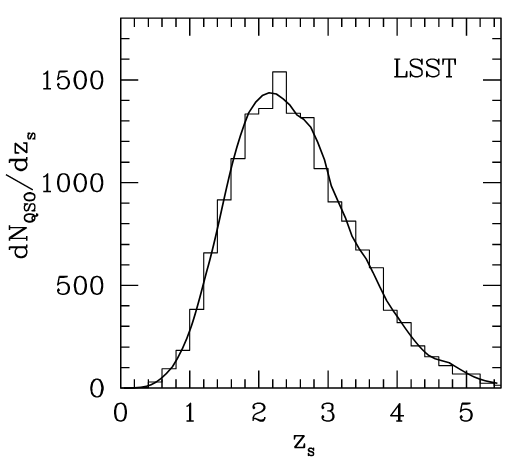
Oguri & Marshall 2010
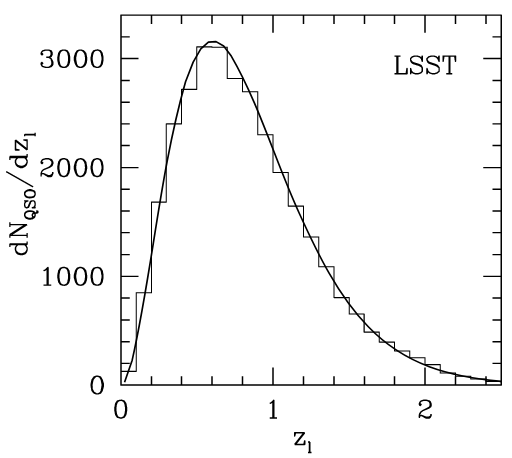
\( z_{\text{obs}} \)= 0.0 \( z_{\text{lens}} \)= 0.5 \( z_{\text{src}} \)= 2.0
Ray-Tracing
* Nan Li + 16
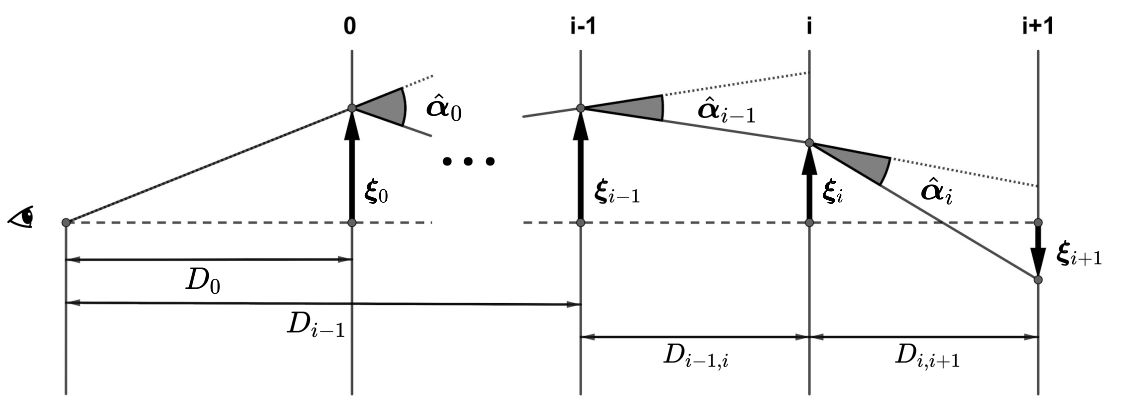
- use PICS* to find lensed images
- 10 lens-planes in redshift space
- truncated Singular Isothermal Ellipsoid (SIE) lens profile
- create catalogue for 1000 double and 400 quadruple imaged sources
Lens-Modelling
Gravlens*
SIE
(10 param.)
Glafic**
Softened Power-Law (SPL)
(11 param.)
lens-model:
cross-validate
*Gravlens by Keeton, **Galfic by Oguri
input:
perturbation: constant shear
image-positions, -time delays, -magnifications, redshifts
errors on input: assume best observation conditions (sub-%)
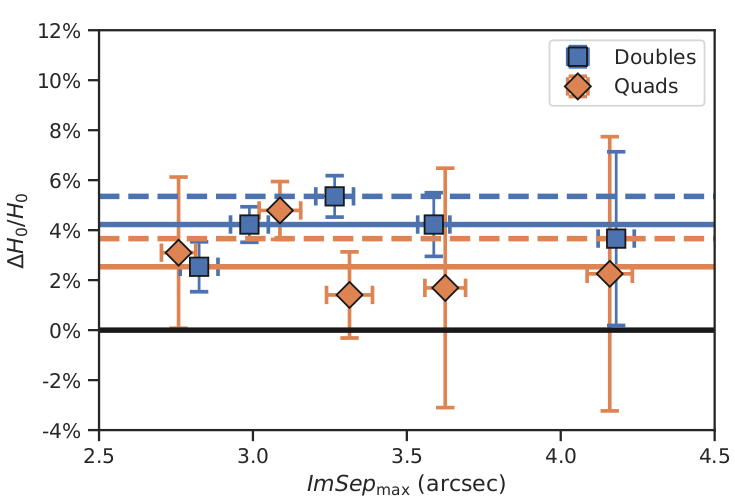
\( H_0 \) Estimate
prior on \( H_0 \) = [0.2, 1.2]
\( H_0 \) Estimate
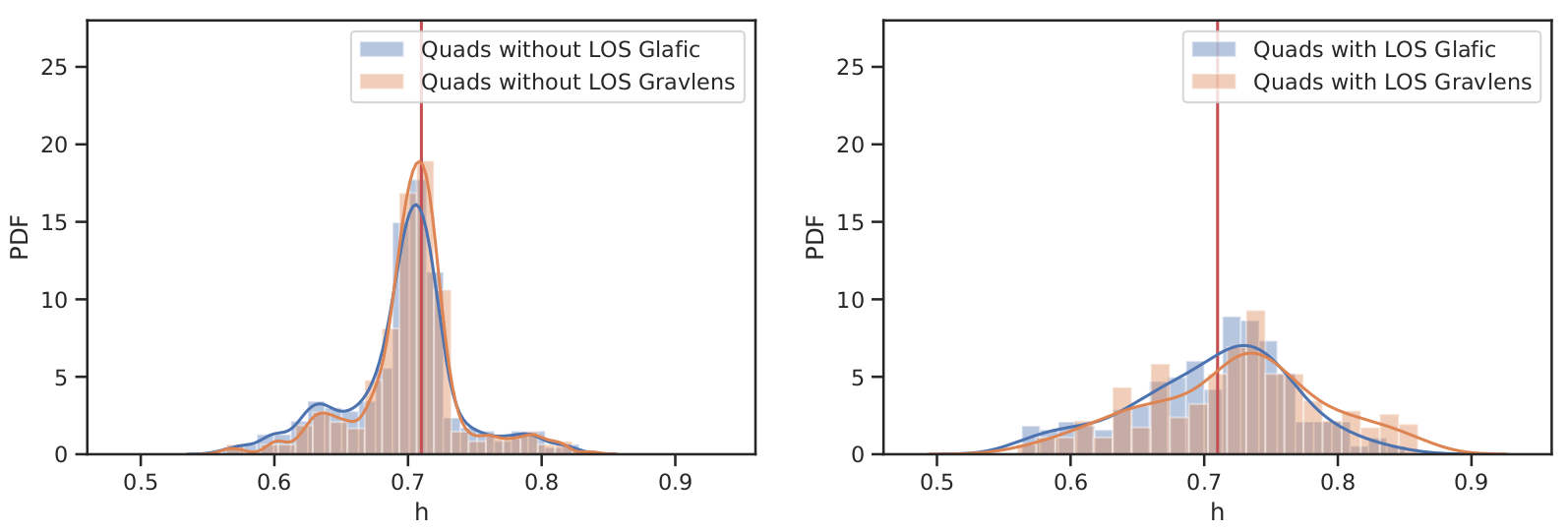
\( H_0 \) Estimate
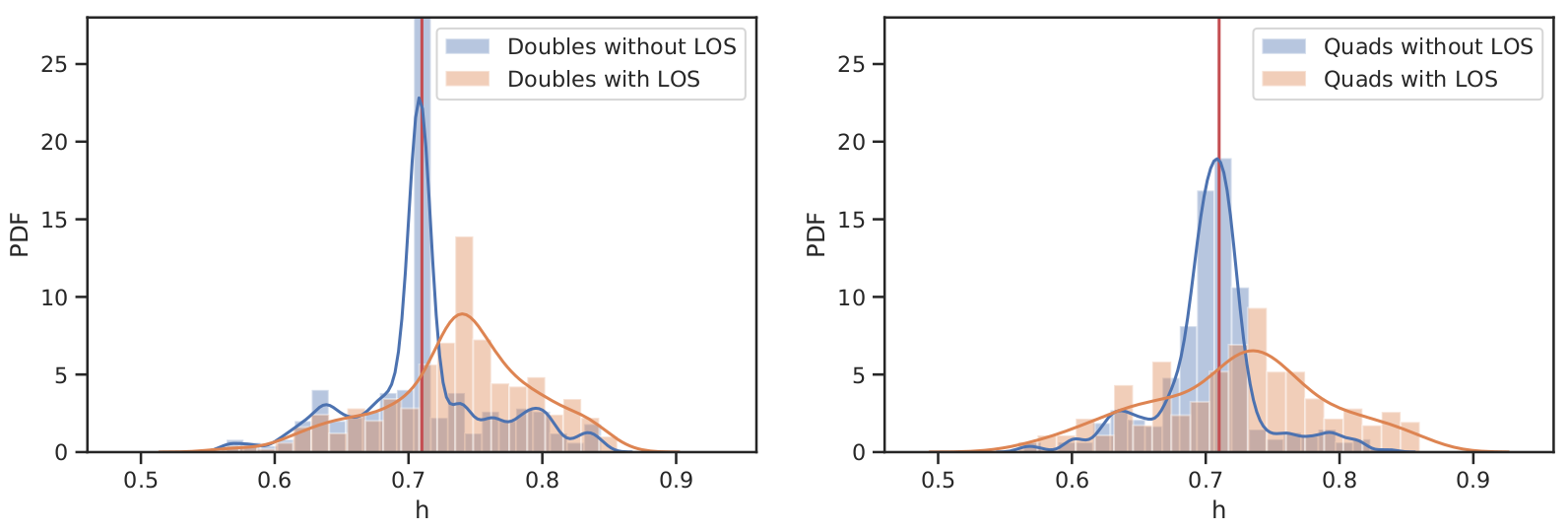
\( H_0 \) Estimate
Argonne National Laboratory (USA/IL)
Physics: Gravity
Volume: \( 4.225 \text{Gpc}^3 \)
Particle Nr.: \( 10240^3 \)
Dark matter resolution: \( \sim 2.6 10^9 M_{\odot} \)
Light-Cone
Semi-Analytic model named cosmoDC2*:
- designed for LSST-DESC
- based on Outer Rim Simulations
- \( 500 \text{deg}^2 \)
- \( z = 0 - 3 \)
- Halo mass = \( 10^{10} - 10^{15} M_{\odot} \)
- Stellar mass = \( 10^{8} - 10^{13} M_{\odot} \)
- including positions, redshift, orientations, ellipticity, colors of the galaxies in a given light cone
*github.com/LSSTDESC/cosmodc2
How to measure \( H_0 \)
Observed:
- Image-positions
- Magnitudes
- (Spectra)
- Time-delay
- Redshift
- (Lens mass)
Modelled:
- mass
- position
- ellipticity
- P.A.
- shear
- ...

S. Suyu + 14
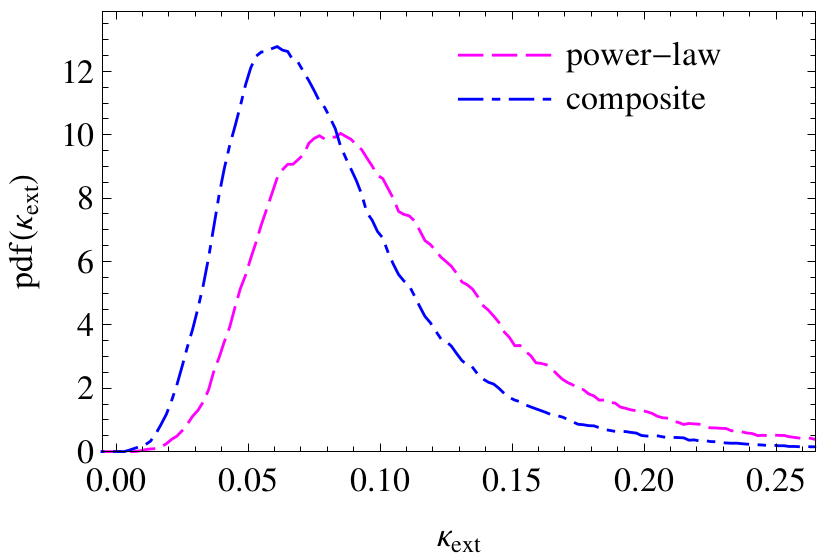
PDF from Millenium Simulation
Estimating \( \kappa_{\text{ext}} \)
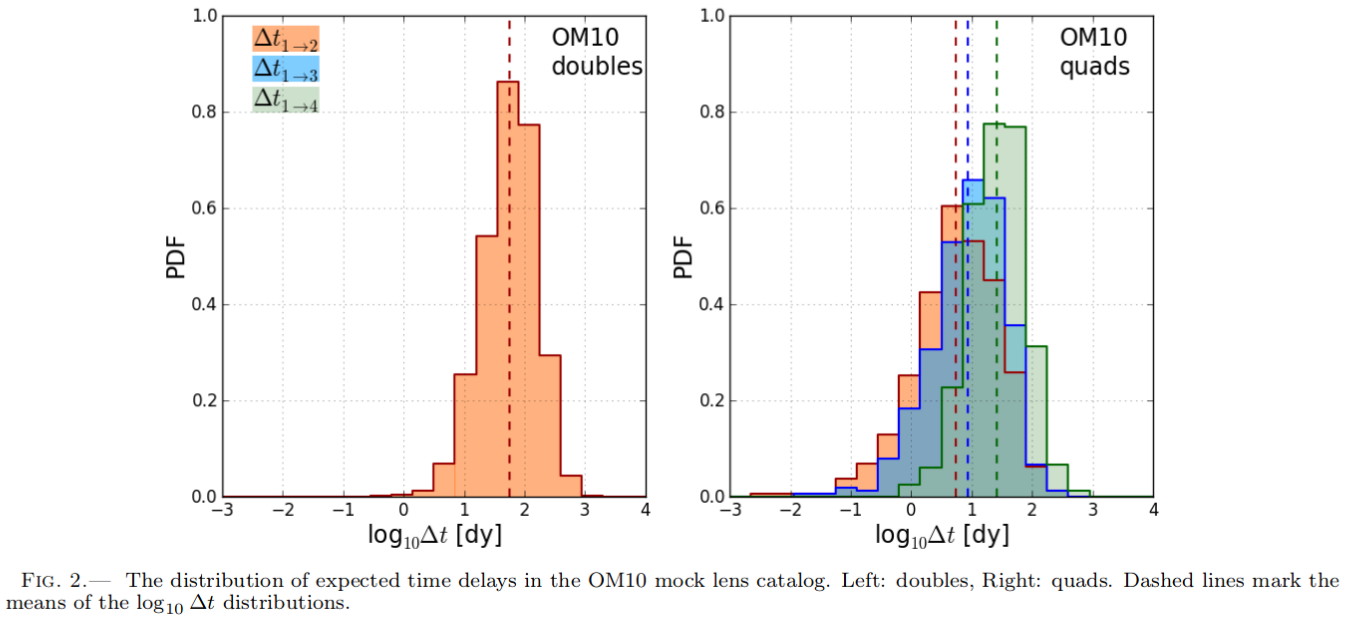
Gregory Dobler et al. 2014
Time Delays
How to measure \( H_0 \)
More variables than knows !!!
Options 1:
Collect better data
Options 2:
Collect more data
Fermat Potential difference
Observable
Goal
Inferable
Observable
Goal
Inferable